
Figure 1: Aristotle's categories
The art of ranking things in genera and species is of no small importance and very much assists our judgment as well as our memory. You know how much it matters in botany, not to mention animals and other substances, or again moral and notional entities as some call them. Order largely depends on it, and many good authors write in such a way that their whole account could be divided and subdivided according to a procedure related to genera and species. This helps one not merely to retain things, but also to find them. And those who have laid out all sorts of notions under certain headings or categories have done something very useful.Gottfried Wilhelm von Leibniz, New Essays on Human Understanding
Abstract. For centuries, philosophers have sought universal categories for classifying everything that exists, lexicographers have sought universal terminologies for defining everything that can be said, and librarians have sought universal headings for storing and retrieving everything that has been written. During the 1970s, the ANSI SPARC committee proposed the three-schema architecture for defining and integrating the database systems that manage the world economy. Today, the semantic web has enlarged the task to the level of classifying, labeling, defining, finding, integrating, and using everything on the World Wide Web, which is rapidly becoming the universal repository for all the accumulated knowledge, information, data, and garbage of humankind. This talk surveys the issues involved, the approaches that have been successfully applied to small systems, and the ongoing efforts to extend them to distributed, interconnected, rapidly growing, heterogeneous systems.
Contents:
This paper consists of excerpts from previously published articles
by John F. Sowa, updated with new material about ongoing projects
on ontology and their implications for databases, knowledge bases,
and the semantic web. For more background on these and related topics,
see the book
Knowledge Representation.
1. What is Ontology?
The subject of ontology is the study of the categories of things that exist or may exist in some domain. The product of such a study, called an ontology, is a catalog of the types of things that are assumed to exist in a domain of interest D from the perspective of a person who uses a language L for the purpose of talking about D. The types in the ontology represent the predicates, word senses, or concept and relation types of the language L when used to discuss topics in the domain D. An uninterpreted logic is ontologically neutral: It imposes no constraints on the subject matter or the way the subject is characterized. By itself, logic says nothing about anything, but the combination of logic with an ontology provides a language that can express relationships about the entities in the domain of interest.
Aristotle's Categories. The word ontology comes from the Greek ontos for being and logos for word. It is a relatively new term in the long history of philosophy, introduced by the 19th century German philosophers to distinguish the study of being as such from the study of various kinds of beings in the natural sciences. The traditional term for the types of beings is Aristotle's word category, which he used for classifying anything that can be said or predicated about anything. In the first treatise in his collected works, Aristotle presented ten basic categories, which are shown at the leaves of the tree in Figure 1. That tree is based on a diagram by the Viennese philosopher Franz Brentano (1862).

Figure 1: Aristotle's categories
To connect the categories of Figure 1, Brentano added some terms taken from other works by Aristotle, including the top node Being and the terms at the branching nodes: Accident, Property, Inherence, Directedness, Containment, Movement, and Intermediacy.
Genus and Differentiae. The oldest known tree diagram was drawn in the 3rd century AD by the Greek philosopher Porphyry in his commentary on Aristotle's categories. Figure 2 shows a version of the Tree of Porphyry, as it was drawn by the 13th century logician Peter of Spain. It illustrates the subcategories under Substance, which is called the supreme genus or the most general supertype.
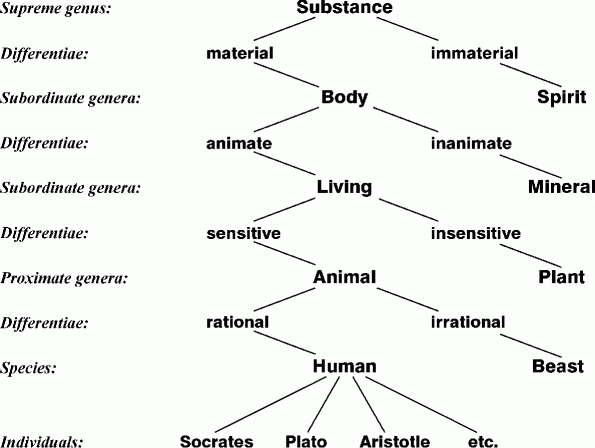
Figure 2: Tree of Porphyry
Despite its age, the Tree of Porphyry has many features that are considered quite modern. Following is Porphyry's description:
Substance is the single highest genus of substances, for no other genus can be found that is prior to substance. Human is a mere species, for after it come the individuals, the particular humans. The genera that come after substance, but before the mere species human, those that are found between substance and human, are species of the genera prior to them, but are genera of what comes after them.
Aristotle used the term διαφορα (in Latin, differentia) for the properties that distinguish different species of the same genus. Substance with the differentia material is Body and with the differentia immaterial is Spirit. The technique of inheritance is the process of merging all the differentiae along the path above any category: LivingThing is defined as animate material Substance, and Human is rational sensitive animate material Substance. Aristotle's method of defining new categories by genus and differentiae is fundamental to artificial intelligence, object-oriented systems, the semantic web, and every dictionary from the earliest days to the present.
Syllogisms. Besides his categories for representing ontology, Aristotle developed formal logic as a precise method for reasoning with them and about them. His major contribution was the invention of syllogisms as formal patterns for representing rules of inference. The following table lists the names of the four types of propositions used in syllogisms and the corresponding sentence patterns that express them.
| Type | Name | Pattern |
|---|---|---|
| A | Universal affirmative | Every A is B. |
| I | Particular affirmative | Some A is B. |
| E | Universal negative | No A is B. |
| O | Particular negative | Some A is not B. |
With letters such as A and B in the sentence patterns, Aristotle introduced the first known use of variables in history. Each letter represents some category, which the Scholastics called praedicatum in Latin and which became predicate in English. If necessary, the verb form is may be replaced by are, has, or have in order to make grammatical English sentences. Although the patterns may look like English, they are limited to a highly stylized or constrained syntax, which is sometimes called controlled natural language. Such language can be read as if it were natural language, but the people who write it must have some training before they can write it correctly. The advantage of controlled language is that it can be automatically analyzed by computer and be translated to logic.
To make the rules easier to remember, the medieval Scholastics developed a system of mnemonics for naming and classifying them. They started by assigning the vowels A, I, E, and O to the four basic types of propositions. The letters A and I come from the first two vowels of the Latin word affirmo (I affirm), and the letters E and O come from the word nego (I deny). These letters are the vowels used in the names of the valid types of syllogisms. The following table shows examples of the four types of syllogisms named Barbara, Celarent, Darii, and Ferio. The three vowels in each name specify the types of propositions that are used as the two premises and the conclusion.
|
| ||||||||||||||||
|
|
Barbara, Celarent, Darii, and Ferio are the four types of syllogisms
that make up Aristotle's first figure. Another fifteen types
are derived from them by rules of conversion, which change
the order of the terms or the types of statements.
Barbara and Darii are the basis for the modern
rule of inheritance in type hierarchies.
Celarent and Ferio are used to detect and reason about constraints
and constraint violations in a type hierarchy. Those four rules are
also the foundation for a subset of first-order logic called
description logic, two versions of which are DAML and OIL.
2. Some Modern Systems
Philosophers often build their ontologies from the top down with grand conceptions about everything in heaven and earth. Programmers, however, tend to work from the bottom up. For their database and AI systems, they often start with limited ontologies or microworlds, which have a small number of concepts that are tailored for a single application. The blocks world with its ontology of blocks and pyramids has been popular for prototypes in robotics, planning, machine vision, and machine learning.
For the Chat-80 question-answering system, David Warren and Fernando Pereira designed an ontology for a microworld of geographical concepts. The hierarchy in Figure 3 shows the Chat-80 categories, which were used for several related purposes: for reasoning, they support inheritance of properties from supertypes to subtypes; for queries, they map to the fields and domains in a database; and for language analysis, they determine the constraints on permissible combinations of nouns, verbs, and adjectives. Yet Figure 3 is specialized for a single application: rivers and roads are considered subtypes of lines; and bridges, towns, and airstrips are treated as single points.

Figure 3: Geographical categories in the Chat-80 system
For Chat-80, the restrictions illustrated in Figure 3 simplified both the analyzer that interpreted English questions and the inference engine that computed the answers. But the simplifying assumptions that were convenient for Chat-80 would obscure or eliminate details that might be essential for other applications.
Although many database and knowledge-based systems are considerably larger than Chat-80, the overwhelming majority of them have built-in limitations that prevent them from being merged and shared with other projects. Banks, for example, have a large number of similar concepts, such as CheckingAccount, SavingsAccount, Loan, and Mortgage. Yet when two banks merge, there are so many inconsistencies in the detailed specifications of those concepts that the resulting database is always the disjoint union of the original databases. Any actual merging is usually accomplished by canceling all the accounts of one type from one bank, transferring the funds, and recreating totally new accounts in the format of the other bank.
Conceptual Schema. The need for standardized ways of encoding knowledge has been recognized since the 1970s. The American National Standards Institute (ANSI) proposed that all pertinent knowledge about an application domain should be collected in a single conceptual schema (Tsichritzis & Klug 1978). Figure 4 illustrates an integrated system with a unified conceptual schema at the center. Each circle is specialized for its own purposes, but they all draw on the common application knowledge represented in the conceptual schema. The user interface calls the database for query and editing facilities, and it calls the application programs to perform actions and provide services. Then the database supports the application programs with facilities for data sharing and persistent storage. The conceptual schema binds all three circles together by providing the common definitions of the application entities and the relationships between them.

Figure 4: Conceptual schema as the heart of an integrated system
For more than twenty years, the conceptual schema has been important for integrated application design, development, and use. Unfortunately, there were no full implementations. Yet partial implementations of some aspects of the conceptual schema have formed the foundation of several important developments: the fourth generation languages (4GLs); the object-oriented programming systems (OOPS); and the tools for computer-aided software engineering (CASE). Each of these approaches enhances productivity by using and reusing common data declarations for multiple aspects of system design and development. Each of them has been called a solution to all the world's problems; and each of them has been successful in solving some of the world's problems. But none of them has achieved the ultimate goal of integrating everything around a unified schema. One programmer characterized the lack of integration in a poignant complaint:
Any one of those tools by itself is a tremendous aid to productivity.The latest attempt to integrate all the world's knowledge is the semantic web. So far, its major contribution has been to propose XML as the common syntax for everything. That is useful, but the problems of syntax are almost trivial in comparison to the problems of developing a common or at least a compatible semantics for everything.
But any two of them together will kill you.
Large Ontologies. At the opposite extreme from a microworld limited to a small domain, the Cyc system (Lenat & Guha 1990; Lenat 1995) was designed to accommodate all of human knowledge. Its very name was taken from the stressed syllable of the word encyclopedia. Figure 5 shows two dozen of the most general categories at the top of the Cyc hierarchy. Beneath those top levels, Cyc contains about 100,000 concept types used in the rules and facts encoded in its knowledge base.
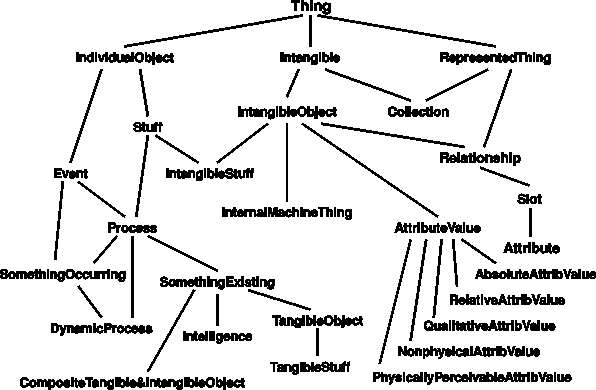
Figure 5: Top-level categories used in Cyc
The following three projects have developed the largest ontologies that are currently available:
Porphyry began the practice of drawing trees to represent hierarchies of categories, but more general acyclic graphs are needed to represent an arbitrary partial ordering, such as the subtype-supertype relation between categories. In this paper, Figures 1, 2, and 3 are trees, in which every node except the top has a single parent node. Figure 5 for the Cyc ontology is an acyclic graph, in which some nodes have more than one parent. Such graphs support multiple inheritance, since a node can inherit properties from any or all of its parents. Figure 6 shows three kinds of graphs for representing partial orderings: a tree, a lattice, and an arbitrary acyclic graph. To simplify the drawings, a common convention is to omit the arrows that show the direction of the ordering and to assume that the lower node represents a subtype of the higher node.

Figure 6: A lattice, a tree, and an acyclic graph
The term hierarchy is often used indiscriminately for any partial ordering. Some authors use the term hierarchy to mean a tree, and tangled hierarchy to mean an acyclic graph that is not a tree. In general, every tree is an acyclic graph, and every lattice is also an acyclic graph; but most lattices are not trees, and most trees are not lattices. In fact, the only graphs that are both trees and lattices are the simple chains (which are linearly ordered). Formally, a lattice is a mathematical structure consisting of a set L, a partial ordering such as the subtype-supertype relation, and two operators that represent the supremum or least common upper bound and the infimum or greatest common lower bound. For more detail about lattices and related structures, see the tutorial on math and logic.
Figure 7 shows a hierarchy of top-level categories defined by Sowa (2000), based on the distinctions observed by a number of philosophers, especially Charles Sanders Peirce and Alfred North Whitehead. The categories are derived by combinations of three ways of partitioning or subdividing the top category T: Physical or Abstract (P, A); Independent, Relative, or Mediating (I, R, M); Continuant or Occurrent (C, O). Each of the other categories is a synonym for the combination of categories from which it was derived: Object, for example, could be represented by the abbreviation PIC for Physical Independent Continuant; and Purpose would be AMO for Abstract Mediating Occurrent. At the bottom of Figure 7, the absurd type ^, which represents the contradictory conjunction of all categories. It completes the hierarchy by serving as a subtype of every other type.

Figure 7: Hierarchy generated by the top three distinctions
To avoid making the diagram too cluttered, the hierarchy in Figure 7 omits some of the possible combinations. The full lattice would be generated by taking all possible combinations of the three basic distinctions, but in many lattices, some of the possible combinations are not meaningful. The following table of beverages, which is taken from a paper by Michael Erdmann (1998), illustrates a typical situation in which many combinations do not occur. Some combinations are impossible, such as a beverage that is simultaneously alcoholic and nonalcoholic. Others are merely unlikely, such as hot and sparkling.
| Attributes | |||||
|---|---|---|---|---|---|
| Concept Types | nonalcoholic | hot | alcoholic | caffeinic | sparkling |
| HerbTea | x | x | |||
| Coffee | x | x | x | ||
| MineralWater | x | x | |||
| Wine | x | ||||
| Beer | x | x | |||
| Cola | x | x | x | ||
| Champagne | x | x | |||
Table of beverage types and attributes
To generate the minimal lattice for classifying the beverages in the above table, Erdmann applied the method of formal concept analysis (FCA), developed by Bernhard Ganter and Rudolf Wille (1999) and implemented in an automated tool called Toscana. Figure 8 shows the resulting lattice; attributes begin with lower-case letters, and concept types begin with upper-case letters.
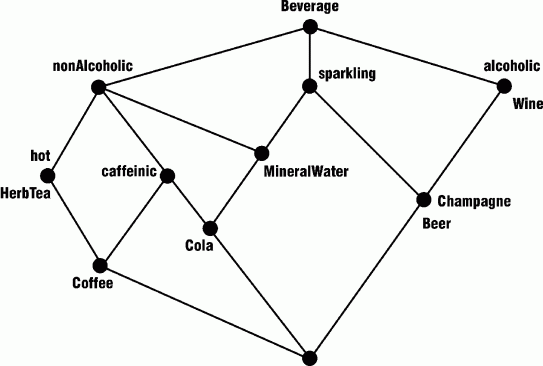
Figure 8: Lattice constructed by the method of formal concept analysis
In Figure 8, beer and champagne are both classified at the same node, since they have exactly the same attributes. To distinguish them more clearly, wine and champage could be assigned the attribute madeFromGrapes, and beer the attribute madeFromGrain. Then the Toscana system would automatically generate a new lattice with three added nodes:

Figure 9: Revised lattice with new attributes
Note that the attribute nonalcoholic is redundant, since it is the complement of the attribute alcoholic. If that attribute had been omitted from the table, the FCA method would still have constructed the same lattice. The only difference is that the node corresponding to the attribute nonalcoholic would not have a label. In a lattice for a familiar domain, such as beverages, most of the nodes correspond to common words or phrases. In Figure 9, the only node that does not correspond to a common word or phrase in English is sparkling&alcoholic.
Lattices are especially important for representing ontologies and
for revising, refining, and sharing ontologies. They are just
as useful at the lower levels of the ontology as they are
at the topmost levels. Each addition of a new distinction
or differentia results in a new lattice, which is called
a refinement of the previous lattice.
The first lattices were introduced by Leibniz, who generated all
possible combinations of the basic distinctions.
A refinement generated by FCA contains only the minimal number of nodes
needed to accommodate the new attribute and its subtypes.
Leibniz's method would introduce superfluous nodes, such as
hot & caffeinic & sparkling & madeFromGrapes.
The FCA lattices, however, contain only the known concept types
and likely generalizations, such as sparkling & alcoholic.
For this example, Leibniz's method would generate a lattice of 64 nodes,
but the FCA method generates only 14 nodes. A Leibniz-style of lattice
is the ultimate refinement for a given set of attributes, and
it may be useful when all possible combinations must be considered.
But the more compact FCA lattices avoid the nonexistent combinations.
4. Notations for Logic
To express anything that has been or will be represented requires a universal language ¾ one that can represent anything and everything that can be said. Fortunately, universal languages do exist. There are two kinds:
The problem of relating different systems of logic is complex, but it has been studied in great depth. In one sense, there has been a de facto standard for logic for over a century. In 1879, Gottlob Frege developed a tree notation for logic, which he called the Begriffsschrift. In 1883, Charles Sanders Peirce independently developed an algebraic notation for predicate calculus, which with a change of symbols by Giuseppe Peano, is the most widely used notation for logic today. Remarkably, these two radically different notations have identical expressive power: anything stated in one of them can be translated to the other without loss or distortion.
Even more remarkably, the classical first-order logic (FOL) that Frege and Peirce developed a century ago has proved to be a fixed point among all the variations that logicians and mathematicians have invented over the years. FOL has enough expressive power to define all of mathematics, every digital computer that has ever been built, and the semantics of every version of logic including itself. Fuzzy logic, modal logic, neural networks, and even higher-order logic can be defined in FOL. Every textbook of mathematics or computer science attests to that fact. They all use a natural language as the metalanguage, but in a form that can be translated to two-valued first-order logic with just the quantifiers " and $ and the basic Boolean operators. Besides expressive power, first-order logic has the best-defined, least problematical model theory and proof theory, and it can be defined in terms of a bare minimum of primitives: just one quantifier (either " or $) and one or two Boolean operators. Even subsets, such as Horn-clause logic or Aristotelian syllogisms, are more complicated, in the sense that more detailed definitions are needed to specify what cannot be said in those subsets than to specify everything that can be said in full FOL.
The power of FOL and the prestige of its adherents have not deterred philosophers, logicians, linguists, and computer scientists from developing other logics. For various purposes, modal logics, higher-order logics, and other extended logics have many desirable properties:
Since the semantics of FOL was firmly established by Alfred Tarski's model theory in 1935, the only thing that has to be standardized is notation. But notation is a matter of taste that raises the most heated arguments and disagreements. To minimize the arguments, the NCITS L8 committee on Metadata has been developing two different notations with a common underlying semantics. ndard, and any concrete notation that conforms to the abstract syntax can be used as an equivalent. To determine conformance, two concrete notations are also being standardized at the same time:
To illustrate the KIF and CG notations, Figure 10 shows a conceptual graph that represents the sentence "John is going to Boston by bus." The CG has four concept nodes: [Go], [Person: John], [City: Boston], and [Bus]. It has three conceptual relation nodes: (Agnt) relates [Go] to the agent John, (Dest) relates [Go] to the destination Boston, and (Inst) relates [Go] to the instrument bus.

Figure 10: CG for "John is going to Boston by bus."
In addition to the graphic display form shown in Figure 10, there is also a formally defined conceptual graph interchange form (CGIF), which serves as a linear representation that can be conveniently stored and exchanged between different implementations:
[Go: *x] [Person: 'John' *y] [City: 'Boston' *z] [Bus: *w] (Agnt ?x ?y) (Dest ?x ?z) (Inst ?x ?z)
The CGIF notation also has a very direct mapping to KIF:
(exists ((?x Go) (?y Person) (?z City) (?w Bus))
(and (Name ?y 'John) (Name ?z 'Boston)
(Agnt ?x ?y) (Dest ?x ?z) (Inst ?x ?w)))
For a list of the relations that connect the concepts corresponding
to verbs to the concepts of their participants, see the
web page
on thematic roles.
The CG in Figure 10 corresponds to a logical form that has only two operators: conjunction and the existential quantifier. To illustrate negation and the universal quantifier, the following table shows the four proposition types used in syllogisms and their representation in CGIF and KIF.
| Pattern | CGIF | KIF |
|---|---|---|
| Every A is B. | [A: @every *x] [B: ?x] | (forall ((?x A)) (B ?x)) |
| Some A is B. | [A: *x] [B: ?x] | (exist ((?x A)) (B ?x)) |
| No A is B. | ~[ [A: *x] [B: ?x] ] | (not (exist ((?x A)) (B ?x))) |
| Some A is not B. | [A: *x] ¬[ [B: ?x] ] | (exist ((?x:A)) (not (B ?x)) |
The four statement types illustrated in the above table represent the kinds of statements used in syllogisms, which are a small subset of full first-order logic. A larger subset, called Horn-clause logic, is used in the if-then rules of expert systems. Following is an example of such a rule, as express in the language Attempto Controlled English (ACE):
If a borrower asks for a copy of a book and the copy is available and LibDB calculates the book amount of the borrower and the book amount is smaller than the book limit and a staff member checks out the copy to the borrower then the copy is checked out to the borrower.The ACE language can be read as if it were English, but it is a formal language that can be automatically translated to logic. Following is the translation to CGIF:
(Named [Entity: *f] [String: "LibDB"])
[If: (Of [Copy: *b] [Book])
(Of [BookAmount: *g] [Borrower: *a])
[BookLimit: *i] [StaffMember: *k]
[Event: (AskFor ?a ?b)]
[State: (Available ?b)]
[Event: (Calculate ?f ?g)]
[State: (SmallerThan ?g ?i)]
[Event: (CheckOutTo ?k ?b ?a)]
[Then: [State: (CheckedOutTo ?b ?a)]]]
And following is the translation to KIF:
(exist ((?f entity))
(and (Named ?f 'LibDB)
(forall ((?a borrower) (?b copy) (?c book) (?g bookAmount)
(?i bookLimit) (?k staffMember) (?d ?h ?l ?e ?j))
(if (and (of ?b ?c) (of ?g ?a)
(event ?d (askFor ?a ?b))
(state ?e (available ?b))
(event ?h (calculate ?f ?g))
(state ?j (smallerThan ?g ?i))
(event ?l (checkOutTo ?k ?b ?a)) )
(exist (?m) (state ?m (checkedOutTo ?b ?a))) ))))
Besides the combinations used in syllogisms and Horn-clause logic,
conceptual graphs and KIF support all the possible combinations
permitted in first-order logic with equality. They can also be
used as metalevel languages, which can be used to represent a much
richer version of logic, including modal and intentional logics.
For more examples, see the
translation
of English sentences to CGs, KIF, and predicate calculus.
For the theoretical foundation of these extensions, see the book
Knowledge Representation
by John Sowa.
5. Ontology Sharing and Merging
Knowledge representation is the application of logic and ontology to the task of constructing computable models for some application domain. Each of the three basic fields ¾ logic, ontology, and computation ¾ presents a different class of problems for knowledge sharing:
To address such problems, standards bodies, professional societies, and industry associations have developed standards to facilitate sharing. Yet the standards themselves are part of the problem. Every field of science, engineering, business, and the arts has its own specialized standards, terminology, and conventions. Yet the various fields cannot be isolated: medical instruments, for example, must be compatible with the widely divergent standards developed in the medical, pharmaceutical, chemical, electrical, and mechanical engineering fields. And medical computer systems must be compatible with all of the above plus the standards for billing, inventory, accounting, patient records, scheduling, email, networks, databases, and government regulations. The first requirement is to develop standards for relating standards.
The problems of aligning the terms from different ontologies are essentially the same as the problems of aligning words from the vocabularies of different natural languages. As an example, Figure 11 shows the concept type Know, which represents the most general sense of the English word know, and two of its subtypes. On the left are the German concept type Wissen and the French concept type Savoir, which correspond to the English sense of knowing-that. On the right are the German Kennen and the French Connâitre, which correspond to the English sense of knowing-some-entity.
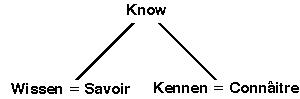
Figure 11: Refinement of Know and its French and German equivalents
Figure 12 shows a more complex pattern for the senses of the English words river and stream and the French words fleuve and rivière. In English, size is the feature that distinguishes river from stream; in French, a fleuve is a river that flows into the sea, and a rivière is either a river or a stream that flows into another river. In translating French into English, the word fleuve maps to the French concept type Fleuve, which is a subtype of the English type River. Therefore, river is the closest one-word approximation to fleuve; if more detail is necessary, it could also be translated by the phrase river that runs into the sea. In the reverse direction, river maps to River, which has two subtypes: one is Fleuve, which maps to fleuve; and the other is BigRivière, whose closest approximation in French is the word rivière or the phrase grande rivière.
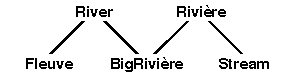
Figure 12: Hierarchy for River, Stream, and their French equivalents
Even when two languages have words that are roughly equivalent in their literal meanings, they may be quite different in salience. In the type hierarchy, Dog is closer to Vertebrate than to Animal. But since Animal has a much higher salience, people are much more likely to refer to a dog as an animal than as a vertebrate. To illustrate the way salience affects word choice, Figure 13 shows part of the hierarchy that includes the English Vehicle and the Chinese Che, which is represented by the character at the top of the hierarchy. That character was derived from a sketch of a simple two-wheeled cart: the vertical line through the middle represents the axle, the horizontal lines at the top and bottom represent the two wheels, and the box in the middle represents the body. Over the centuries, that simple concept has been generalized to represent all wheeled conveyances for transporting people or goods.

Figure 13: Hierarchy for English Vehicle and Chinese Che
The English types Car, Taxi, Bus, Truck=Lorry, and Bicycle are subtypes of Vehicle. The Chinese types do not exactly match the English ones: Che is a supertype of Vehicle that includes Train (HuoChe), which is not usually considered a vehicle in English. The type QiChe includes Taxi (ChuZuQiChe) and Bus (GongGongQiChe) as well as Car, which has no specific word that distinguishes it from a taxi or bus.
In English, the specific words car, bus, or taxi are commonly used in speech, and the generic vehicle would normally be used only in a technical context, such as traffic laws. In Chinese, however, the word che is the most common term for any kind of a vehicle. When the specific type is clear from the context, a Chinese speaker would simply say Please call me a che, I'm waiting for the 5 o'clock che, or I parked my che around the corner. The fact that che is both a stand-alone word and a component of all its subtypes enhances its salience; and the fact that chuzuqiche and gonggongqiche are four-syllable words decreases their salience. Therefore, it would sound unnatural to use the word chuzuqiche, literally the exact equivalent of taxi, to translate the sentence Please call me a taxi. In translations from Chinese, the type Che would have to be specialized to an appropriate subtype in order to avoid sentences like I parked my wheeled conveyance around the corner.
Misalignments between ontologies arise from a variety of cultural, geographical, linguistic, technical, and even random differences. Geography probably contributes to the French distinction, since the major rivers in France flow into the Atlantic or the Mediterranean. In the United States, however, there are major rivers like the Ohio and the Misouri, which flow into the Mississippi. The Chinese preference for one-syllable morphemes that can either stand alone or form part of a compound leads to the high salience for che, while the English tendency to drop syllables leads to highly salient short words like bus and taxi from omnibus and taxicab.
The issues illustrated in Figures 11, 12, and 13 represent inconveniences, but they do not create inconsistencies in the merged ontology. They can be resolved by refining one or both ontologies by adding more concept types that represent the union of all the distinctions in both ontologies that were merged. Figure 14 shows a "bowtie" inconsistency that sometimes arises in the process of aligning two ontologies.
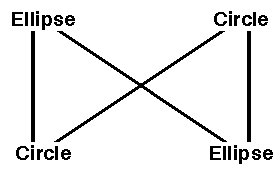
Figure 14: A bowtie inconsistency between two ontologies
On the left of Figure 14, Circle is represented
as a subtype of Ellipse, since a circle can be considered
a special case of an ellipse in which both axes are equal.
On the right is a representation that is sometimes used
in object-oriented programming languages: Ellipse is
considered a subclass of Circle, since it has more complex methods.
If both ontologies were merged, the resulting hierarchy would have
an inconsistency. To resolve such inconsistencies, some definitions
must be changed, or some of the types must be relabeled.
In most graphics systems, the mathematical definition of Circle
as a subtype of Ellipse is preferred because it supports
more general transformations.
6. Glossary
This glossary summarizes the terminology of methods and techniques for defining, sharing, and merging ontologies. These definitions, which were written by John F. Sowa, are based on discussions in the ontology working group of the NCITS T2 Committee on Information Interchange and Interpretation.
As an example, a black cat and an orange cat would be considered very similar as instances of the category Animal, since their common catlike properties would be the most significant for distinguishing them from other kinds of animals. But in the category Cat, they would share their catlike properties with all the other kinds of cats, and the difference in color would be more significant. In the category BlackEntity, color would be the most relevant property, and the black cat would be closer to a crow or a lump of coal than to the orange cat. Since prototype-based ontologies depend on examples, it is often convenient to derive the semantic distance measure by a method that learns from examples, such as statistics, cluster analysis, or neural networks.
All bibliographical references have been moved to the combined bibliography for this web site.
Send comments to John F. Sowa.
Last Modified: