
The purpose of this note is to show that under a small number of assumptions, it is possible to interpret truth in a context as a quantification over truth in a set of 'atomic' contexts, which are transparent to all the connectives. We also analyze the necessary assumptions, and suggest conditions under which they are intuitively reasonable.
The primary sources of the relevant intuitions, and much of the formal technique, are mereology and earlier work on temporal truth; and the thinking herein all arises from looking at contexts as having parts, and allowing for the possibility that a sentence may be true in some parts of a context but not all of the parts. These matters have all been previously analyzed in considerable depth in the case where a context is a time-interval, and indeed one can follow the entire development with that intuition as a guide. However, the actual formal assumptions used amount to only six axioms, and so the results apply to any notion of context which satisfies these.
This entire note is inspired by the context logic originally introduced by J. McCarthy and R. V. Guha, and subsequently developed by others. It is intended to address the issue discussed in [MHF06], viz. the transparency of contextual assertions to the propositional connectives.
The central construction of context logic is ist(c P). Here, c denotes a context, which is supposed to be a 'bearer of truth' in some broad sense, and P denotes a proposition, which is some entity that can be said to be true or false in a context. A proposition may fail to have a truth-value in a context, so that ist(c P) and ist(c ~P) might both be false.
Examples of contexts include time-intervals, where ist means that the proposition holds during the time-interval; believers, in which ist means that the proposition is believed; information sources such as databases, in which ist means that the information source is a provenance for the proposition; and modal-alternative, imaginary or counterfactual worlds or states of affairs, in which ist asserts that a proposition is true in the state of affairs. Most of the intuitions underlying the development in this note arise from the first application, where contexts are thought of as time-intervals, but the formal results apply to any kind of context which satisfies the axioms.
It is generally assumed that ist distributes over conjunctions in its second argument: that is, that ist(c P&Q) implies ist(c P) and ist(c Q). It is easy to see intutively that this corresponds to the idea that the proposition P is true throughout the context c. However, not all attributions of truth to a situation distribute over conjunction. For example, a recent day of hard travelling might be summarized by saying "On April 30 I was in seven states" meaning, of course, that I was at various times of the day in one of seven states, not that I was in all seven states all of the day. In this case, the relevant notion of 'truth in' seems to not distribute over conjunction: for
(true-in 300405 (I am in Texas)) & (true-in 300405 (I am in Mississippi))
can be true, when clearly
(true-in 300405 ((I am in Texas) & (I am in Mississippi)) )
must be false. It is intuitively clear what is meant, however: this is a different notion of 'true in' from the ist sense, and in fact it is precisely the classical dual, definable as
wist(c P) =df ~ist(c ~P)
Clearly, wist distributes over disjunction but not (in general) over conjunction; and true-in, as used above, is wist rather than ist: it means intuitively "at some time during" rather than "throughout".
The relationship between ist and wist is exactly analogous to the usual duality between the universal and existential quantifiers, and between the strong and weak modal operators. In fact, the two operators can be viewed as 'indexed' modalities, withthe particular context providing the index, and the standard transliteration of modal propositional logic into first-order logic then maps them into patterns of quantification. If we think of a context as a time-interval, and a time-interval as a set of points, then ist(c P) translates into for all p in c, P(p), and wist(c P) translates into there exists a p in c with P(p). This kind of translation provides for a useful and natural reduction of 'ist' language to a simpler subcase where the basic relationship between a proposition and a 'context-point' is transparent to all the connectives and hence merges ist and wist into a single relationship, which we could paraphrase as 'P is true at c'. The various cases of truth-in-a-context being opaque to the connectives, such as the example given above of wist(c P&Q) not being identical in meaning to wist(c P) & wist(c Q) , can then all be explained by the patterns of quantification; in this case, the fact that exists (x) (P(x) & Q(x) is not logically equivalent to (exists (x) P(x) & exists (x) Q(x)). Propositional context logic then reduces to classical quantifier logic plus a very simple, completely transparent, notion of true-at-a-context-point.
The purpose of this note is to identify some general conditions under which this reduction of contexts to sets of context-points can be done. We will show that a small number of axioms, only one of which is at all controversial, suffice.
Following this analogy with modal logic, and to reduce notational clutter in what follows, we will adopt modality-style notation and write [c]P for ist(c P) and <c>P for wist(c P); the brackets are intended to suggest the box-diamond notation commonly used to indicate modalities.
Formally, the letters P, Q, etc. are understood to range over a set P of propositions - which we will assume is closed under the usual operations of negation and conjunction, i.e. is a Boolean algebra - and c, d, etc, over a set C of all contexts, and we assume that there is a relationship between these sets represented by the notation [c]P for c in C and P in P.
We use colors to distinguish definitions, axioms and lemmas.
We have the definition:
d1. <c>P =df ~ [c](~P)
The first axiom is the basic assumption about ist, that it distributes over conjunction.
a1. [c](P & Q) iff ( [c]P and [c]Q )
The second is a kind of internal coherence principle for contexts, that an overt contradiction cannot be true throughout a context:
a2. ~ [c](P & ~P)
An elementary result in classical modal logic then follows:
Lemma 1. [c]P implies <c>P
Proof. Assume [c]P, and suppose ~<c>P. By d1, [c]~P. By a1, [c](P & ~P); by a2, this is a contradiction. So <c>P by modus tollens. QED
Now, we introduce a relationship of parthood on contexts. Intuitively, a part of a context is some piece or aspect of it which is also considered to be a context, and can be distinguished by there being a proposition which has a different truthvalue in that part than in some other part. In the case of a time-interval, parthood seems to correspond naturally to being a subinterval. We will write c<d for the parthood relationship, which we will assume is transitive, asymmetric and reflexive, i.e. a partial order:
a3. < is a partial order
a3a. (e<d & d<c) implies e<c
a3b. (d<c and c<d) implies c=d
a3c. c<c
To be true throughout a context, then, is to be true throughout all of its parts, giving another basic axiom:
a4. ([c]P and d<c) implies [d]P
This simply identifies [c] as the 'strong' modality of the dual pair. It is easy to see that this has an alternative formulation:
a4a. [c]P iff (for all d<c, [d]P)
since 'if' is trivial, because c<c.
We need a stronger way to relate truth in a context with parthood of a context. After some exploration of possibilities, the following seems to be the most reasonable assumption which is sufficient to establish the results. We christen this the truth locating axiom. It is discussed at greater length below.
a5. (TLA). <c>P implies there exists a d<c with [d]P
(This can be stated as an "iff" since "if" is a consequence of earlier axioms.)
Finally, we will assume that parthood of contexts satisfies a basic axiom of mereology, the supplementation axiom:
d2. c0d =df c overlaps d =df there exists an e with e<c and e<d
a6. (SUPP). c<d or there is an e with e<c and ~(e0d)
Axioms a1 through a6 are all that we require to show that any context can be viewed as a set of context-points. (If we assume that contexts and propositions satisfy a certain extensionality condition, then axioms a5 and a6 become interderivable, reducing the total number of assumptions needed. This possibility is discussed below.)
The following equivalences show that axiom a4a can be re-cast, assuming the TLA, into a stronger form:
[c]P iff
~<c>~P iff
~(exists d<c with [d]~P) iff
for all d<c, ~[d]~P iff
for all d<c, <d>P
so:
Lemma 2: [c]P iff (for all d<c, [d]P) iff (for all d<c, <d>P)
The most important consequence of the TLA is that every context must somewhere make a commitment to any proposition:
Lemma 3: For all c there is a d<c with [d]P or [d]~P
Proof. By a2, ~[c](P & ~P) so by a1, ~[c]P or ~[c]~P , i.e. <c>~P or <c>P, so by the TLA the result follows. QED
Context-points are constructed from nests, i.e. descending chains of subcontexts. This construction is closely related to the classical ultrafilter/ideal technique for constructing points from partial order structures, widely used in topology and underlying the Stone representation theorem for Boolean algebras. (It may be that the classical results can be utilized to prove the required result directly, but the author was not able to perform this feat.)
The intuitive picture behind these definitions is that such a nest either determines the truthvalues of all propositions or else can be extended by adding a subcontext which determines a new proposition: so by taking the limit, we can view any sufficiently deep nest as a 'point' which fully determines the truthvalue of every proposition, and so is transparent to negation. We then say that a point is inside a context when the nest contains the context (since, intuitively, any nest determines a point which is inside all the contexts in the nest, as the figure illustrates), and identify a context with the set of all such points inside it.

d3. nest =df totally ordered subset of C =df a set n of contexts with for all c,d in n, c<d or d<c
d4. n is bounded =df c is the bound of n =df c in n and for all d in n, c<d
d5. P is true at n =df (n)P =df for some c in n, [c]P
d6. x is a point =df x is a nest and for every P in P, either (x)P or (x)~P
d7. x is inside c =df d<c for some d in x
Here, d5 provides the definition of 'truth at a point'. We use the neutral notation (n)P rather than [n]P to emphasise the distinction between points (nests) and contexts, and also because, as shown below, the strong and weak forms of ist coincide for points, i.e. ~(n)P iff (n)~P. Notice that in d7, c is not required to be in the nest x (as the above figure also illustrates).
The main result is a consequence of the TLA and the axiom of choice:
Lemma 4. Every bounded nest is a subset of a point
Proof. Say that P is determined by c when [c]P or [c]~P, and let n be a bounded nest with bound b. By the axiom of choice, we can assume that P is well-ordered. If n is not a point then let P be the first proposition in the well-ordering which is not determined by b, then by lemma 3 there is a d<b with [d]P or [d]~P, so (n union {d}) is a bounded nest which determines a superset of the propositions determined by n. By induction, the limit of this construction is a nest which determines every proposition in P. QED.
The boundedness condition is necessary; the lemma is not true for arbitrary nests, as shown by this example: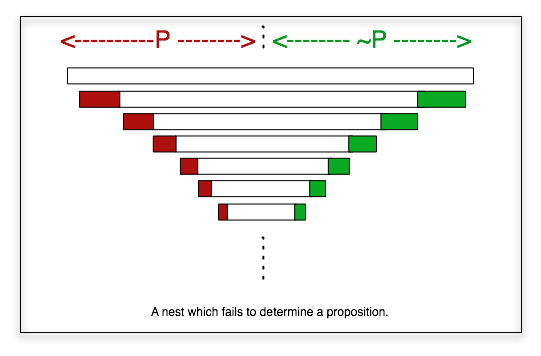
This is the well-known example of the interval-endpoint when a light switches off [Allen&Hayes89]. Note that although every context in the nest has subcontexts c and d with [c]P and [d]~P, so satisfying the TLA, and the whole construction satisfies the supplementation axiom 6, nevertheless the center chain of subcontexts is itself a nest which avoids these cases and so fails to determine P. The construction in the proof of the lemma cannot generate this nest, of course.
Since the singleton set of any context is a bounded nest, Lemma 4 can be re-stated as: any context has a point inside it.
Points – in fact, nests generally – are transparent to conjunction, like contexts:
Lemma 5. (n)(P & Q) iff (n)P and (n)Q
Proof. If (n)(P & Q) then for some c in n, [c](P & Q), so [c]P and [c]Q, so (n)P and (n)Q. If (n)P and (n)Q, then for c, d in u, [c]P and [d]Q, and either d<c or c<d. Assume c<d; then [c]P & [c]Q by a4, so [c](P & Q) by a1; so (u)(P & Q); and similarly if d<c. QED.
Since points determine the truthvalues of all propositions, they are also transparent to negation, and hence to all the propositional connectives:
Lemma 6. If x is a point then (x)~P iff not (x)P
Proof. If (x)P and (x)~P then (x)(P & ~P) so for some c in x, [c](P & ~P), contradicting a2. So not ((x)P and (x)~P). But either (x)P or (x)~P, since x is a point. So not (x)P iff (x)~P. QED
If P holds anywhere in a context then it must hold at a point in the context:
Lemma 7. <c>P iff there is a point x inside c with (x)P
Proof. Suppose c
in x and (x)P; then there is a d with [d]P and c<d or d<c, so
either [c]P or there is a d<c with [d]P; so <c>P.
Now suppose that <c>P; then by the TLA, there is a d<c with
[d]P. {c,d} is a bounded nest with bound d, so by lemma 4 there is a
point x inside d, hence inside c. Since x contains d, (x)P. QED
It follows that truth throughout a context, i.e. the ist case, is exactly truth at all points inside the context:
[c]P iff
~<c>~P iff
~(exists x inside c with (x)~P) iff
for all x inside c, ~(x)~P iff
for all x inside c, (x)P
Finally, it remains to show that discriminating points are sufficient to map the subcontext relation into the subset relation on sets of points.
Lemma 8. c<d iff every point x inside c is also inside d
Proof. If c<d and x is inside c, then x is inside d by d7 and a3a.
Now suppose not c<d; then by SUPP there is an e with e<c and not e0d. Then {c,e} is a bounded nest, so there is a point p inside e, so inside c. If x is inside d, then e and d would be in a nest, so d<e or e<d, so e0d; so, x is not inside d. QED
This establishes the main result we required: if we think of a context as the set of points inside the context, then:
The proof of the if half of lemma 8 is the only place where the mereological axiom of supplementation, a6, is used. Intuitively, the role of this axiom is to prohibit 'gratuitous' cases of parthood where a context c is declared to be a 'larger' than another context d – that is, d<c and not c<d – but there is no way to distinguish any part of c that is not also part of d. This axiom can be replaced by a different assumption which ensures that any 'external' part of a context must be identifiable by a suitable proposition. The truth locating axiom a5 then has a6 as a consequence. We state this as an axiom, but note that it is not required for the above results, but represents an alternative assumption.
a7.(Separation) c<d or there is a P in P with [d]P and ~[c]P
A consequence of this is that if, for every P in P, [c]P iff [d]P, then c=d. That is, C satisfies an extensionality condition with respect to the propositions in P: two contexts differ only if they somewhere assign a different truth-value to some proposition, which we can call the separating proposition.
Separation prohibits gratuitous distinctions between contexts which would be invisible to the set of propositions; supplementation prohibits gratuitous distinctions which would be invisible to the set of contexts. Perhaps unsurprisingly, therefore, the supplementation axiom a6 can be derived directly from the TLA and separation:
Lemma. a1-a5 plus a7 entail a6
Proof. Suppose ~(c<d), then by a7 there is a P with [d]P and ~[c]P, i.e. <c>~P; so by a5, there is an e<c with [e]~P, so ~(e0d) by a2 and a3. QED
As this proof makes clear, the supplementation axiom can be viewed intuitively as a special case of the TLA, in which the proposition P is the assertion part of d but not part of c. The separation assumption gives this viewpoint some flesh by insisting that a suitable proposition to capture this distinction must exist. The analogy seems to provide some insight into the similar thinking that underlies both axioms: there need to be enough 'parts' in the universe of parts to make certain distinctions explicit as a distinction between parts themselves. Put another way, the set of parts needs to be rich enough to provide sufficient granularity to be able to 'see' all distinctions that are relevant to parthood or truth.
One can argue that if the set of contexts does not satisfy separation, it can be replace it with an equivalent set which does, by taking the quotient under the obvious equivalence. For c,d in C, define c = d to mean: ([c]P iff [d]P) for all P in P. Clearly this is an equivalence relation, and if we take the quotient of C under = and define [x]P to mean [c]P for all c in the equivalence class x, then the resulting context space is indistinguishable from C as far as the truth of any proposition in P is concerned, and satisfies a7 by construction. Thus, the separation axiom is in a sense trivial, since it can always be satisfied: it amounts to accepting the idea that differences between contexts which make no difference to the truth of propositions can be ignored, when we are dealing with questions concerning truth of propositions. When considering semantics of a language, this amounts to the observation that to assume, as part of the general semantic conditions, that contexts separate propositions expressed by sentences of the language, is a reasonable semantic constraint; for any interpretation which failed this condition could be replaced by a quotient structure which satisfies it, without changing the truthvalue of any sentence. This argument would be less compelling, however, for a language which allowed other means that the use of sentences to express propositions; for example, if it allowed for quantification over propositions.
If the propositions are expressed using a vocabulary which itself contains a symbol denoting the subcontext relation and in which it is possible to refer to contexts and quantify over them, then separation is automatic, since one can express the necessary proposition directly in terms of the contexts themselves: it amounts to part of d but not part of c. This amounts to the assumption that for every context one can formulate a sentence which is necessarily true throughout that context.
An example of the conditions under which separation holds for temporal contexts is the presence of a clock. If we think of a clock as a source of propositions which state the clock time 'now', and are true just at the time-point the proposition is asserted by the clock, then the resulting set of propositions is sufficient to separate any set of time-intervals down to the resolution provided by the clock (for example, to the nearest second, say). Another example might be contexts which are the episodes in a story or narrative, considered as subcontexts of the entire story, and separated by sentences or phrases in the text which describe some distinctive event or circumstance which is unique to that episode, and therefore can be used to refer to it, in a phrase like "that weekend when Joe came to the ranch to court Millie and the dog caught fire". In belief contexts, contexts which could not be separated would be those which were indistinguishable to the believer, so separation amounts to the assumption that distinct states of belief can somehow be characterized as states in which distinct propositions are believed.
The above shows that TLA is closely related to the mereological axiom of supplementation. It is also closely related to the Hausdorff property of topological spaces. If we think of <c>P as saying that there is a point in c where P is true, and [c]P as saying that c is an open set throughout which P is true, then the TLA has the consequence that if <c>P and <c>~P, i.e. if there are two points in c which are propositionally distinguishable, then there are non-overlapping open sets d and e surrounding those points. Separation requires that any two distinct points will be propositionally separable, so this applies to any two distinct points: which is exactly the Hausdorff property.
It might be thought that the TLA rules out examples such as "The light came on at some time during the afternoon", where a proposition is true at a single point in an interval; but that conclusion would be mistaken, since the d in the axiom might itself be a single point (or a set containing a single point). What the TLA requires, in cases such as this, is that C – in this example, the set of of time-intervals – includes subcontexts which are small enough to be the exact time referred to in the sentence – in this case, the time when the light came on. If there are propositions which are true only at isolated points, then the space of contexts must provide those point-like contexts. Another way to put it is that the space of time-contexts must provide for phrases such as "When P, Q" which can be understood as referring to the subcontext when P is true. This intuitively accords with the idea that the purpose of subcontexts is to be the repositories of patterns of truth: that a subcontext is in a sense identifiable as a 'place' where some propositions are true but others may not be.
The significance of the TLA can be illustrated by a possible counterxample, which might be called the 'irrational oscillator'. Let C be the set of subintervals of the unit interval on the reals, and suppose P is true at all irrational points and false at all rational points. Then <c>P is always true and [c]P always false, for any c. This fails to satisfy the TLA by the truth being too finely scattered, preventing a single 'piece' of it to be isolated by a context-point with enough precision. By assuming the TLA, therefore, we are excluding examples like this, where truth is more finely distributed than the set of context-parts is able to discriminate. Note however that if we took C instead to be the subsets of the unit interval, rather than merely the subintervals – or even if we took it to merely include closed single-point intervals [t,t] for every irrational t – then the TLA would be satisfied. Thus, the failure of this example to satisfy the TLA can be attributed to its failure to include enough context-parts in the space C of contexts.
All of the above discussion is based on, and motivated by, an overarching intuition which thinks of contexts as entities which have an extent and which can therefore be thought of as having parts. This is an essentially spatial metaphor, well suited to notions of context which are essentially spatio-temporal; what Menzel [Menzel99] calls 'objective' contexts. This topological/mereological framework seems less obviously well suited to more epistemic or psychological notions of context, however.
Take for example the idea of a document or information source as a context, where ist(c,P) is supposed to mean that the proposition P is asserted more or less directly by the source c. (Notice the required change from being true in a context to being asserted by a context.) Or, to take a related and popular example, suppose a context is understood to be a work of fiction, and ist(c,P) means something like that P would hold in the "imaginary world" described by the fiction c. (We are here using "world" in the informal sense in which one might speak of "the world of Conan Doyle", rather than the modal-semantic sense of "possible world".) In cases like this, it is far from clear what the relation of context-parthood could be understood to mean, or whether the formal assumptions we have used would apply. Even such a basic axiom as a2 might well be false when discussing psychological states, source documents or fictions, none of which are required to be internally consistent; and certainly, the links we have noted to mereology and topology are far less convincing when applied to such cases. There seems to be no plausible reason why states of belief or fictional "worlds" should satisfy anything like the Hausdorff condition, for example.
It is very difficult to come up with any assumptions which are both sufficiently nontrivial to support any useful level of mathematical or meta-theoretic analysis, and also seem to be plausible across all the proposed uses of the 'context' idea and the ist(c,P) notation. The main conclusion of this note, therefore, is to reiterate a thesis proposed some time ago: that there is no single useful idea of "context", and in order to construct nontrivial theories of contextual truth, it is necessary to distinguish different conceptions of context. In this spirit, then, the formal results are offered as a first step towards a useful theory of spatiotemporal contextualization, with an accompanying suggestion that it might be useful to try to characterize the basic assumptions of other notions of context and contextualization of truth in the same formal, axiomatic style.
Chris Menzel suggested the proof strategy used in lemma 4.
Allen, J. & Hayes, P. (1989) "Moments and Points in an Interval-Based Temporal Logic". Computational Intelligence, 5, 225-238
Buvac, S., Buvac, V. & Mason, I. (1995) "Metamathematics of Context", Fundamentae Informaticae 23(3), pp 263-301
Guha, R. V. (1991) Contexts: A Formalization and some Applications. Thesis, Stanford University; Technical report STAN-CS-91-1399-Thesis
Makarios, S., Heuer, K & Fikes, R. (2006) Computatinal Context Logic and Species of $ist$. Unpublished memorandum, Stanford Knwledge Systems Laboratory KSL-06-07
McCarthy, J. (1993) "Notes on Formalizing Context', Proc. 13th International Joint Conference on Artificial Intelligence
McCarthy, J. & Buvac, S. (1998), "Formalizing Context (Expanded Notes)", in Computing Natural Language (ed. Aliseda, van Glabeek & Westerstahl), CSLI Lecture Notes vol. 81, CSLI Publications, Stanford University.
Menzel, C. (1999) "The objective conception of context and its logic", Minds and Machines 9 (1999), pp 29-56